|
Ellipses
and Circles : CDC,
Arc, ArcTo, Pie, Chord, AngleArc
|
| |
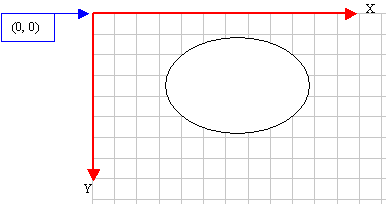
An
ellipse is a closed continuous line whose points
are positioned so that two points exactly opposite
each other have the exact same distant from a
central point. It can be illustrated as follows:
Because
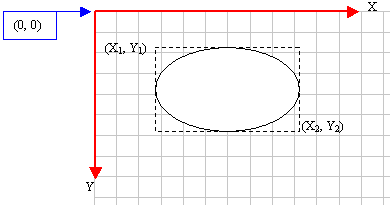
an ellipse can fit in a rectangle, in GDI
programming, an ellipse is defined with regards to
a rectangle it would fit in. Therefore, to draw an
ellipse, you specify its rectangular corners. The
syntax used to do this is:
BOOL Ellipse(int x1, int y1, int x2, int y2);
The
arguments of this method play the same roll as
those of the Rectangle() method:
Here
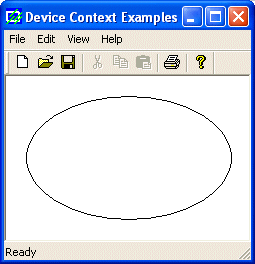
is an example:
void CExoView::OnDraw(CDC* pDC)
{
pDC->Ellipse(20, 20, 226, 144);
}
|
 |
Like
the rectangle, you can draw an ellipse using a
RECT or CRect object it would fit in. The syntax
you would use is:
BOOL Ellipse(LPCRECT lpRect);
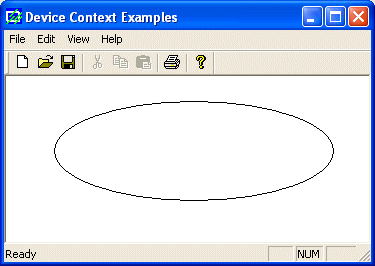
Here
is an example:
void CExoView::OnDraw(CDC* pDC)
{
CRect Recto(328, 125, 48, 25);
pDC->Ellipse(&Recto);
}
|
 |
A
circle is an ellipse whose all points have the
same distance with regards to a central point.
|
Round
Rectangles and Round Squares
|
| |
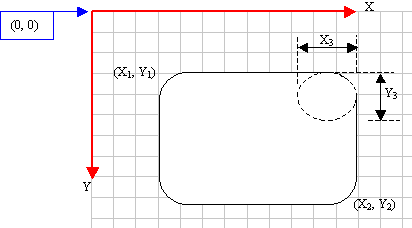
A
rectangle qualifies as round if its corners do not
form straight angles but rounded corners. It can
be illustrated as follows:
To
draw such a rectangle, you can use the CDC::RoundRect()
method. Its syntaxes are:
BOOL RoundRect(int x1, int y1, int x2, int y2, int x3, int y3);
BOOL RoundRect(PCRECT lpRect, POINT point);
When
this member function executes, the rectangle is
drawn from the (x1, y1) to
the (x2, y2) points. The
corners are rounded by an ellipse whose width
would be x3 and the ellipse's height
would be x3.
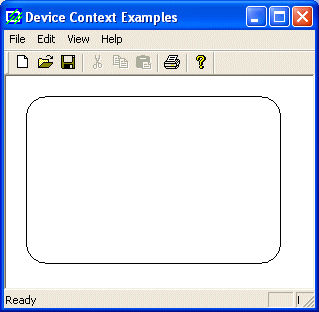
Here
is an example:
void CExoView::OnDraw(CDC* pDC)
{
pDC->RoundRect(20, 20, 275, 188, 42, 38);
}
|
 |
A
round square is a square whose corners are
rounded.
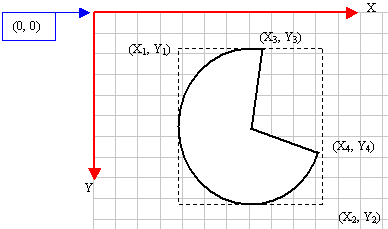
A
pie is a fraction of an ellipse delimited by two
lines that span from the center of the ellipse to
one side each. It can be illustrated as follows:
To
draw a pie, you can use the CDC::Pie()
method whose syntaxes are:
BOOL Pie(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4);
BOOL Pie(LPCRECT lpRect, POINT ptStart, POINT ptEnd);
The
(x1, y1) point determines
the upper-left corner of the rectangle in which
the ellipse that represents the pie fits. The (x2,
y2) point is the bottom-right corner of
the rectangle. These two points can also be
combined in a RECT or a CRect
variable and passed as the lpRect value.
The
(x3, y3) point, that can
also supplied as a POINT or CPoint for lpStart
argument, specifies the starting corner of the pie
in a default counterclockwise direction.
The
(x4, y4) point, or ptEnd
argument, species the end point of the pie.
To
complete the pie, a line is drawn from (x3,
y3) to the center and from the center
to the (x4, y4) points.
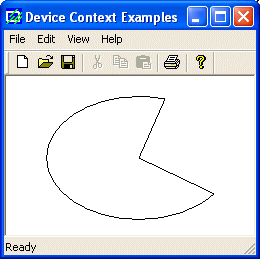
Here
is an example:
void CExoView::OnDraw(CDC* pDC)
{
pDC->Pie(40, 20, 226, 144, 155, 32, 202, 115);
}
|
 |
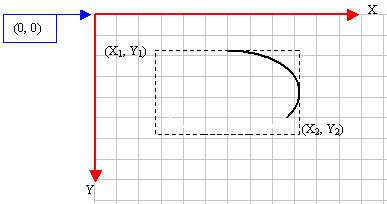
An
arc is a portion or segment of an ellipse, meaning
an arc is a non-complete ellipse. Because an arc
must confirm to the shape of an ellipse, it is
defined as it fits in a rectangle and can be
illustrated as follows:
To
draw an arc, you can use the CDC::Arc()
method whose syntax is:
BOOL Arc(int x1, int y1, int x2, int y2,
int x3, int y3, int x4, int y4);
Besides
the left (x1, y1) and the
right (x2, y2) borders of
the rectangle in which the arc would fit, an arc
must specify where it starts and where it ends.
These additional points are set as the (x3,
y3) and (x4, y4)
points of the figure. Based on this, the above arc
can be illustrated as follows:
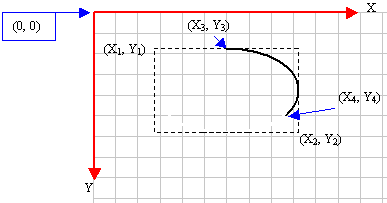
Here
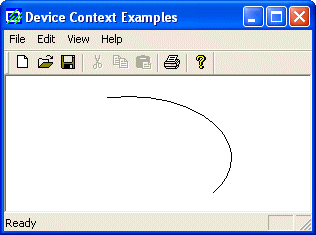
is an example:
void CExoView::OnDraw(CDC* pDC)
{
pDC->Arc(20, 20, 226, 144, 202, 115, 105, 32);
}
|
 |
An
arc can also be drawn using the location and size
of the rectangle it would fit in. Such a rectangle
can be passed to the Arc() method as a RECT
or a CRect object. In this case, you must
define the beginning and end of the arc as two POINT
or CPoint values. The syntax used is:
BOOL Arc(LPCRECT lpRect, POINT ptStart, POINT ptEnd);
Here
is an example that produces the same result as
above:
void CExoView::OnDraw(CDC* pDC)
{
CRect Recto(20, 20, 226, 144);
CPoint Pt1(202, 115);
CPoint Pt2(105, 32);
pDC->Arc(Recto, Pt1, Pt2);
}
Besides
the Arc() method, the CDC class
provides the ArcTo() member function used
to draw an arc. It also comes in two syntaxes as
follows:
BOOL ArcTo(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4);
BOOL ArcTo(LPCRECT lpRect, POINT ptStart, POINT ptEnd);
This
method uses the same arguments as Arc().
The difference is that while Arc() starts drawing
at (x3, y3), ArcTo() does not inherently
control the drawing starting point. It refers to
the current point, exactly like the LineTo()
(and the PolylineTo()) method. Therefore,
if you want to specify where the drawing should
start, can call CDC::MoveTo() before ArcTo().
Here is an example:
void CExoView::OnDraw(CDC* pDC)
{
CRect Recto(20, 20, 226, 144);
CPoint Pt1(202, 115);
CPoint Pt2(105, 32);
pDC->MoveTo(207, 155);
pDC->ArcTo(Recto, Pt1, Pt2);
}
|
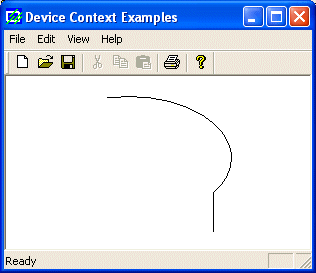 |
Here
is and arc we drew earlier with a call to Arc():
void CExoView::OnDraw(CDC* pDC)
{
pDC->Arc(20, 20, 226, 144, 202, 115, 105, 32);
}
|
 |
You
may wonder why the arc is drawn to the right side
of a vertical line that would cross the center of
the ellipse instead of the left. This is because
the drawing of an arc is performed from right to
left or from bottom to up, in the opposite
direction of the clock. This is known as the
counterclockwise direction. To control this
orientation, the CDC class is equipped with
the SetArcDirection() method. Its syntax
is:
int SetArcDirection(int nArcDirection);
This
method specifies the direction the Arc()
method should follow from the starting to the end
points. The argument passed as nArcDirection
controls this orientation. It can have the
following values:
| |
Value |
Orientation |
| |
AD_CLOCKWISE |
The
figure is drawn clockwise |
| |
AD_COUNTERCLOCKWISE |
The
figure is drawn counterclockwise |
The
default value of the direction is AD_COUNTERCLOCKWISE.
Therefore, this would be used if you do not
specify a direction. Here is an example that uses
the same values as above with a different
orientation:
void CExoView::OnDraw(CDC* pDC)
{
pDC->SetArcDirection(AD_CLOCKWISE);
pDC->Arc(20, 20, 226, 144, 202, 115, 105, 32);
}
|
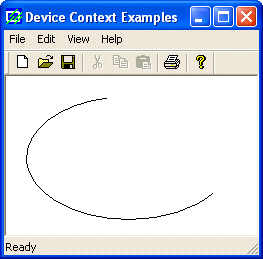 |
After
calling SetArcDirection() and changing the
previous direction, all drawings would use the new
direction to draw arcs using Arc() or ArcTo()
and other figures (such as chords, ellipses, pies,
and rectangles). Here is an example:
void CExoView::OnDraw(CDC* pDC)
{
pDC->SetArcDirection(AD_COUNTERCLOCKWISE);
pDC->Arc(20, 20, 226, 144, 202, 115, 105, 32);
pDC->Arc(10, 10, 250, 155, 240, 85, 24, 48);
}
|
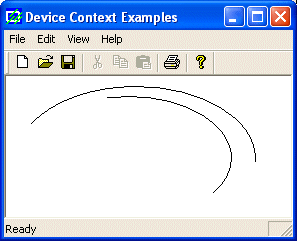 |
If
you want to change the direction, you must call SetArcDirection()
with the desired value. Here is an example;
void CExoView::OnDraw(CDC* pDC)
{
pDC->SetArcDirection(AD_COUNTERCLOCKWISE);
pDC->Arc(20, 20, 226, 144, 202, 115, 105, 32);
pDC->SetArcDirection(AD_CLOCKWISE);
pDC->Arc(10, 10, 250, 155, 240, 85, 24, 48);
}
|
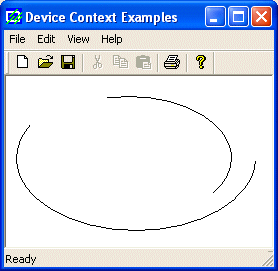 |
At
any time, you can find out the current direction
used. This is done by calling the GetArcDirection()
method. Its syntax is:
int GetArcDirection() const;
This
method returns the current arc direction as AD_CLOCKWISE
or AD_COUNTERCLOCKWISE.
You
can (also) draw an arc using the CDC::AngleArc()
method. Its syntax is:
BOOL AngleArc(int x, int y, int nRadius, float fStartAngle, float fSweepAngle);
This
member function draws a line and an arc connected.
The arc is based on a circle and not an ellipse.
This implies that the arc fits inside a square and
not a rectangle. The circle that would be the base
of the arc is defined by its center located at C(x,
y) with a radius of nRadius. The arc
starts at an angle of fStartAngle. The
angle is based on the x axis and must be positive.
That is, it must range from 0° to 360°. If you
want to specify an angle that is below the x axis,
such as -15°, use 360º-15°=345°. The last
argument, fSweepAngle, is the angular area
covered by the arc.
The
AngleArc() method does not control where it
starts drawing. This means that it starts at the
origin, unless a previous call to MoveTo()
specified the beginning of the drawing.
Here
is an example:
void CExoView::OnDraw(CDC* pDC)
{
pDC->MoveTo(52, 28);
pDC->AngleArc(120, 45, 142, 345, -65);
}
|
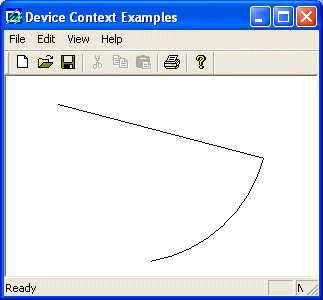 |
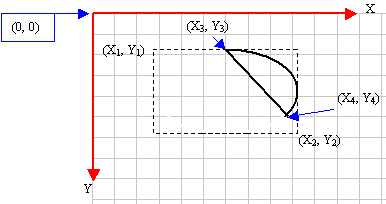
The
arcs we have drawn so far are considered open
figures because they are made of a line that has a
beginning and an end (unlike a circle or a
rectangle that do not). A chord is an arc whose
two ends are connected by a straight line. In
other words, a chord is an ellipse that is divided
by a straight line from one side to another:
To
draw a chord, you can use the CDC::Chord() method.
It is defined as follows:
BOOL Chord(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4);
BOOL Chord(LPCRECT lpRect, POINT ptStart, POINT ptEnd);
The
x1, y1, x2,
and y2 are the coordinates of
the rectangle in which the chord of the circle
would fit. This rectangle can also be defined as a
RECT or a CRect value.
These
x3 and y3
coordinates specify where the arc that holds the
chord starts. These coordinates can also be
defined as the ptStart argument.
The
x4 and y4
that can also be defined as ptEnd specify
the end of the arc.
To
complete the chord, a line is drawn from (x3,
y3) to (x4, y4).
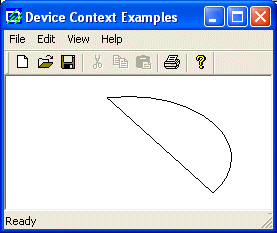
Here
is an example:
void CExoView::OnDraw(CDC* pDC)
{
pDC->Chord(20, 20, 226, 144, 202, 115, 105, 32);
}
|
 |
|





















