WPF 3D Article, Tutorial with Chart Graphics C# Code.

1

When using WPF for 3D graphics, many people have concerns over the performance. Following the guidelines from Microsoft online help, I built a 3D surface chart, as shown in the picture above. The surface chart has more than 40,000 vertices and more than 80,000 triangles. The performance is still fine. The project also includes 3D scatter plot which has a large number of data points. You can build the project, feel the performance of WPF 3D and decide whether WPF 3D is suitable for your 3D data visualization.

2

The WPF 3D is displayed within the Viewport3D UI elements. The three basic components are:

• Camera
• Light
• 3D model

 Collapse | Copy Code

<Window x:Class="WPF Chart.Window1"
    xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
    xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
    Title="WPF 3D Chart" Height="500" Width="600">
    <Grid>
        <Viewport3D Name="mainViewport" >
            <Viewport3D.Camera>
                <OrthographicCamera x:Name="camera" 
                      FarPlaneDistance="10"
	                NearPlaneDistance="1" 
	                LookDirection="0,0,-1"
	                UpDirection="0,1,0"
	                Position="0,0,2" />
            </Viewport3D.Camera>
            <Viewport3D.Children>
                <ModelVisual3D x:Name="Light1">
                    <ModelVisual3D.Content>
                     <DirectionalLight Color="White" Direction="1,1,-1"/>
                    </ModelVisual3D.Content>
                </ModelVisual3D>
            </Viewport3D.Children>
         </Viewport3D>
    </Grid>
</Window>

The root element is a Window. Inside the window, we use Grid layout. Those two elements are provided by Visual Studio when we build the project. Inside the grid, we add a Viewport3D to hold the 3D object. Under theViewport3D, we have a camera, a directional light.

We added the camera and light in the XAML file. Now, we add the 3D model in C# code. The mesh structure (typeSystem.Windows.Media.Media3D.MeshGeometry3D) consists of four parts of data:

1. Vertices location
2. Connection between vertices
3. Normal direction of vertices
4. Texture mapping coordinate of each vertex

The vertices location is represented by a Point3D structure.

 Collapse | Copy Code

System.Windows.Media.Media3D.Point3D point0 = new Point3D(-0.5, 0, 0);
System.Windows.Media.Media3D.Point3D point1 = new Point3D(0.5, 0.5, 0.3);
System.Windows.Media.Media3D.Point3D point2 = new Point3D(0, 0.5, 0);

Those points are put into Positions array of the mesh structure.

 Collapse | Copy Code

System.Windows.Media.Media3D.MeshGeometry3D triangleMesh = new MeshGeometry3D();

triangleMesh.Positions.Add(point0);
triangleMesh.Positions.Add(point1);
triangleMesh.Positions.Add(point2);

Three vertices make a triangle. The vertices connections are described by three integers, which are the indices of the 3 vertices in the Positions array.

 Collapse | Copy Code

int n0 = 0;
int n1 = 1;
int n2 = 2;

The 3 indices of a triangle are added to the TriangleIndices array.

 Collapse | Copy Code

triangleMesh.TriangleIndices.Add(n0);
triangleMesh.TriangleIndices.Add(n1);
triangleMesh.TriangleIndices.Add(n2);

 Collapse | Copy Code

System.Windows.Media.Media3D.Vector3D norm = new Vector3D(0, 0, 1);
triangleMesh.Normals.Add(norm);
triangleMesh.Normals.Add(norm);
triangleMesh.Normals.Add(norm);

 Collapse | Copy Code

System.Windows.Media.Media3D.Material frontMaterial = 
			new DiffuseMaterial(new SolidColorBrush(Colors.Blue));

 Collapse | Copy Code

System.Windows.Media.Media3D.GeometryModel3D triangleModel = 
			new GeometryModel3D(triangleMesh, frontMaterial);

The GeometryModel3D object also has a transform property. We will discuss it in the next section.

 Collapse | Copy Code

triangleModel.Transform = new Transform3DGroup();

 Collapse | Copy Code

System.Windows.Media.Media3D.ModelVisual3D visualModel = new ModelVisual3D();
visualModel.Content = triangleModel;

The ModelVisual3D object will be displayed in Viewport3D:

 Collapse | Copy Code

this.mainViewport.Children.Add(visualModel);

This involves quite a lot of steps. Model3D class in this project helps to generate a ModelVisual3D object. If we run the program, we will see a blue triangle. We cannot rotate it yet. In the next section, we will show how to rotate this 3D model.

3

In this section, we will use the mouse to rotate the 3D model. Rotating the 3D model in WPF is easy, but we want to implement our own selection function later. Therefore, we need to keep a track of the transform when we rotate the 3D model.

In order to catch the mouse event, we cover the Viewport3D with a transparent Canvas. The mouse down, move and up events handlers of the canvas will be added to the window class.

We can either change the camera location or change the transform property of the 3D model to rotate the 3D object. For this project, we will modify the transform property of the 3D model. The transform property of a 3D model can be described as System.Windows.Media.Matrix3D. We will build a special transform class to use this matrix.

 Collapse | Copy Code

public class TransformMatrix
{
   public Matrix3D m_viewMatrix = new Matrix3D();
   private Point m_movePoint;
}

The Matrix3D member variable m_viewMatrix is used to rotate the 3D object. The TransformMatrix class will handle the mouse events and rotate the model.

 Collapse | Copy Code

public class TransformMatrix
{
    public void OnMouseMove(Point pt, System.Windows.Controls.Viewport3D viewPort)
    {
        double width = viewPort.ActualWidth;
        double height = viewPort.ActualHeight;
        if (Keyboard.IsKeyDown(Key.LeftShift) || Keyboard.IsKeyDown(Key.RightShift))
        {
        }
        else
        {
            double aY = 180 * (pt.X - m_movePoint.X) / width;
            double aX = 180 * (pt.Y - m_movePoint.Y) / height;

            m_viewMatrix.Rotate(new Quaternion(new Vector3D(1, 0, 0), aX));
            m_viewMatrix.Rotate(new Quaternion(new Vector3D(0, 1, 0), aY));
            m_movePoint = pt;
        }
    }
}

The 3D rotation is implemented in the mouse move event. The view matrix will rotate according to the offset of the current mouse position and previous mouse position m_movePoint. We scale the rotate so the model moves 180 degrees when we move the mouse from one side of the window to another side. You can change this rotation sensitivity.

To use the TransformMatrix class, we can add a TransformMatrix variable to the window class, and call the mouse event handler of TransformMatrix object at the corresponding mouse events of the window class.

 Collapse | Copy Code

public partial class Window1 : Window
{
    public WPFChart.TransformMatrix m_transformMatrix = new WPFChart.TransformMatrix();
 
    public void OnViewportMouseMove(object sender, 
			System.Windows.Input.MouseEventArgs args)
    {
        Point pt = args.GetPosition(mainViewport);
        if (args.LeftButton == MouseButtonState.Pressed)
        {
            m_transformMatrix.OnMouseMove(pt, mainViewport);
            Transform3DGroup group1 = triangleModel.Transform as Transform3DGroup;
            group1.Children.Clear();
            group1.Children.Add(new MatrixTransform3D(transformMatrix.m_ m_viewMatrix));
        }
    }
}

After we modify the transform matrix, we need to set a new view matrix to the 3D model’s transformproperty.

3. Auto Zoom

The triangle we used in the previous two sections has the data range -0.5 ~ 0.5. The camera we used has a default width of 2. Camera center is at (0, 0). So the triangle is in the camera view range. If the 3D object is out of camera range, the 3D object will not be shown in Viewport3D. We can change the camera position to keep the 3D object in camera view. Here, we use a different approach. We will add another matrix to project the 3D object into the camera view range.

 Collapse | Copy Code

public class TransformMatrix
{
     private Matrix3D m_viewMatrix = new Matrix3D();
     private Matrix3D m_projMatrix = new Matrix3D();

     public Matrix3D m_totalMatrix = new Matrix3D();
}

 Collapse | Copy Code

public class TransformMatrix
{
     public void CalculateProjectionMatrix(double xMin, double xMax, 
		double yMin, double yMax, double zMin, double zMax, double k)
     {
          double xC = (xMin + xMax) / 2;
          double yC = (yMin + yMax) / 2;
          double zC = (zMin + zMax) / 2;
          m_projMatrix.SetIdentity();
          m_projMatrix.Translate(new Vector3D(-xC, -yC, -zC));

          double sX = k*2 / (xMax - xMin);
          m_projMatrix.Scale(new Vector3D(sX, sX, sX));

          m_totalMatrix = Matrix3D.Multiply(m_projMatrix, m_viewMatrix);
     }
}

The last parameter of the function is a scale factor. A value of 0.5 means we want data to take 50% of the screen. Each time, we change the view matrix or projection matrix, we need to calculate the total matrix. We also need to change our code in the window class. Instead of setting the view matrix m_viewMatrix to the 3D model transform property, we will set the total matrix m_totalMatrix to the 3D object transformation.

4. Select in 3D

The WPF provides the mouse hit test function. However, it may not be suitable for a 3D chart. For example, a 3D scatter plot may have several thousand data points. Running hit test on those data points is not practical in terms of performance. Therefore, we should turn off the IsHitTestVisible property of the Viewport3D.

To implement our own selection function, we need to know where a 3D point is projected on the 2D screen. In the previous section, we add a matrix transform to the 3D object. In addition to this transform, the 3D object also goes though other transforms before it is projected onto 2D screen. For example, the camera has its own transform. The orthographic camera we used keeps the default width of 2. It points to the –z direction. You can check the camera transform matrix and will find out that it is an identity matrix. Therefore, we will ignore the camera transform. However, we still have one transform that has not been discussed yet, i.e. the final transform which projects the camera range to Viewport3D.

1. The center of the camera (0, 0) is projected to the center of the Viewport3D (w/2, h/2).
2. The scale factor of transform is decided by x-axis only. Y axis has the same scale as the x-axis.
3. Y axis of the camera points up while the y axis of the Viewport3D points down.

Following those rules, the VertexToScreenPt() function of the TransformMatrix class calculates the screen location of a 3D point.

 Collapse | Copy Code

public class TransformMatrix
{
    public Point VertexToScreenPt(Point3D point, 
		System.Windows.Controls.Viewport3D viewPort)
    {
        Point3D pt2 = m_totalMatrix.Transform(point);

        double width = viewPort.ActualWidth;
        double height = viewPort.ActualHeight;

        double x3 = width / 2 + (pt2.X) * width / 2;
        double y3 = height / 2 - (pt2.Y) * width / 2;

        return new Point(x3, y3);
   }
}

The input Point3D parameter is the 3D location of a point, the return Point value is its location on the 2D screen. To test this function, we will move the mouse onto one corner of the triangle, and compare the actual screen coordinate with predicated position by the VertexToScreenPt() function.

 Collapse | Copy Code

public partial class Window1 : Window
{
    public void OnViewportMouseMove(object sender, 
		System.Windows.Input.MouseEventArgs args)
    {
         Point pt = args.GetPosition(mainViewport);
         if (args.LeftButton == MouseButtonState.Pressed) 
         {
         }
         else
         {
             String s1;
             Point pt2 = m_transformMatrix.VertexToScreenPt
			(new Point3D(0.5, 0.5, 0.3), mainViewport);
             s1 = string.Format("Screen:({0:d},{1:d}), Predicated:({2:d}, 
			H:{3:d})", (int)pt.X, (int)pt.Y, (int)pt2.X, (int)pt2.Y);
             this.statusPane.Text = s1;
         }
    }
}

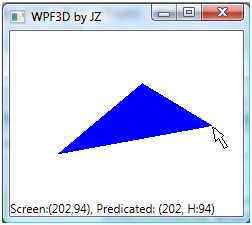
Look at the status pane display, we know TransformMatrix.VertexToScreenPt() function returns the correct screen position. We can rotate the triangle to a different location, and still get matching results. Based on the TransformMatrix.VertexToScreenPt() function, we implement the select function in this project.

Understanding the screen transformation also helps us implement the drag function in mouse move event. The mouse will be used to drag the 3D model when the shift key is down. We want the 3D model to move exactly by the same amount as that mouse move on the screen. Therefore, we use camera width to Viewport3D width ratio as the scale factor when we drag the model.

 Collapse | Copy Code

public class TransformMatrix
{
    public void OnMouseMove(Point pt, System.Windows.Controls.Viewport3D viewPort)
    {
        double width = viewPort.ActualWidth;
        double height = viewPort.ActualHeight;

	if (Keyboard.IsKeyDown(Key.LeftShift) || Keyboard.IsKeyDown(Key.RightShift))
      	{
            double shiftX = 2 *(pt.X - m_movePoint.X) /( width);
            double shiftY = -2 *(pt.Y - m_movePoint.Y)/( width);
            m_viewMatrix.Translate(new Vector3D(shiftX, shiftY, 0));
            m_movePoint = pt;
      	}
         m_totalMatrix = Matrix3D.Multiply(m_projMatrix, m_viewMatrix);
    }
}

5. Basic Classes of the Project

In the previous section, we displayed a triangle. A 3D object consists of many triangles. Mesh3D and ColorMesh3Dclasses in this project are used for single color 3D models and color 3D models respectively. For single color 3D objects, we have the Mesh3D class:

 Collapse | Copy Code

public class Mesh3D
{
     private Point3D [] m_points;            // x, y, z coordinate
     private Triangle3D [] m_tris;           // triangle information
     private Color m_color;                  // mesh color

     public double m_xMin, m_xMax, m_yMin, m_yMax, m_zMin, m_zMax;
}

The single color mesh model consists of an array of 3D points and array of triangle’s vertices’ indices. The whole mesh model has a single color which is described by the third member variable m_color. The last six member variables are the data range of the mesh model.

The Triangle3D class defines the vertex index of a triangle.

 Collapse | Copy Code

public class Triangle3D
{
    public int n0, n1, n2;
}

Based on Mesh3D class, we can build different basic shapes, such as, cube, cylinder, cone, and sphere. They are child classes of Mesh3D class. Those basic shapes are need in 3D charts. 

The Mesh3D class is for data processing. We have to convert it into WPF ModelVisual3D type for 3D display. We also want to merge different mesh models into a single 3D model to enhance the performance of 3D display. TheModel3D class is designed for this purpose. The picture below describes the class structure of this project.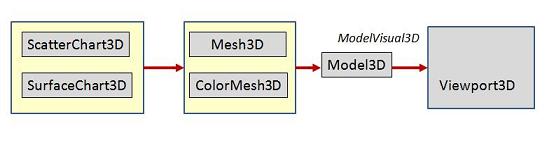 

The 3D data in a different 3D chart has a different form. This project only demos the scatter plot and surface plot. They are represented by ScatterChart3D and SurfaceChart3D classes. The 3D chart data goes through a few conversions before the pass to the Viewport3D. First, it generates an array of Mesh3D (or ColorMesh3D) objects. This Mesh3D array is then passed to the Model3D class and produces a single ModelVisual3D object. The ModelVisual3D object is added to the Viewport3D for display.

6. Color 3D Model

WPF 3D model can set the color using brush. If a 3D chart has many color objects, creating many brushes of different colors will degrade the performance. Instead we can create an image brush for color mapping. The image has a different color at different locations. We can use different mapping coordinates for different colors.

The true color has 256³ = 16777216 colors. Those colors need a 4096x4096 mapping image. Normally, the 3D charts only use limited number of colors. For different 3D charts, we will use different color layouts. For bar chart and scatter plot, we use 16 color values in each channel. There will be 16³ = 4096 colors. This should be enough to mark different categories. The size of the mapping image will be 64x64.

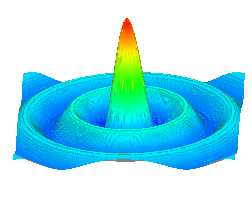
For surface charts, we often pseudo color the surface according to the z value of the 3D plot, as shown in the first picture of this article. The picture below shows the color mapping method we use for pseudo color. The x axis is normalized z value. The y axis shows the RGB color that corresponds to the z value.

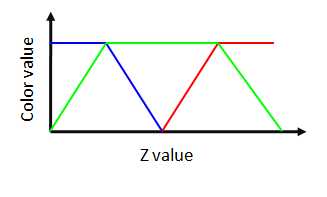
The TextureMapping class implements both color layouts. Here, we only discuss the color layout for scatter plot. You can check the source code of the TextureMapping class for pseudo color mapping. The mapping image has a size of 64x64. The blue channel has 16 values, so the blue channel takes 1/4 of each row. We then change the green channel. For each red value, the green and blue values take 4 rows.

The WritableBitmap will be used in the image brush.

 Collapse | Copy Code

public class TextureMapping
{
    public DiffuseMaterial m_material;
    private void SetRGBMaping()
    {
         WriteableBitmap writeableBitmap = 
		new WriteableBitmap(64, 64, 96, 96, PixelFormats.Bgr24, null);
         writeableBitmap.Lock();

 Collapse | Copy Code

        unsafe
        {
            byte* pStart = (byte*)(void*)writeableBitmap.BackBuffer;
            int nL = writeableBitmap.BackBufferStride;

            for (int r = 0; r < 16; r++)
            {
                for (int g = 0; g < 16; g++)
                {
                    for (int b = 0; b < 16; b++)
                    {
                        int nX = (g % 4) * 16 + b;                            
                        int nY = r*4 + (int)(g/4);

                        *(pStart + nY*nL + nX*3 + 0) = (byte)(b * 17);
                        *(pStart + nY*nL + nX*3 + 1) = (byte)(g * 17);
                        *(pStart + nY*nL + nX*3 + 2) = (byte)(r * 17);
                     }
                }
            }
       }

 Collapse | Copy Code

       writeableBitmap.AddDirtyRect(new Int32Rect(0, 0, 64, 64));

       writeableBitmap.Unlock();

       ImageBrush imageBrush = new ImageBrush(writeableBitmap);
       imageBrush.ViewportUnits = BrushMappingMode.Absolute;
       m_material = new DiffuseMaterial();
       m_material.Brush = imageBrush;
   }
}

Later, when we use mapping image for color painting, we need know the mapping location of a certain color. This is provided by the GetMappingPosition() function of the TextureMapping class.

 Collapse | Copy Code

public class TextureMapping
{
      public Point GetMappingPosition(Color color)
      {
            int r = (color.R) / 17;
            int g = (color.G) / 17;
            int b = (color.B) / 17;

            int nX = (g % 4) * 16 + b;
            int nY = r * 4 + (int)(g / 4);

            return new Point((double)nX /63, (double)nY /63);
      }
}

To use the mapping image for color, we get the color of the each vertex, then find the mapping coordinate of that color, and add the mapping coordinate to the TextureCoordinates array of the MeshGeometry3D object. This is implemented in the SetModel() function of the Model3D class.

Using the Code

This project provides some base classes for high performance 3D charts. It is not a complete library. You still need to add more classes to display grid, label, title. The picture below shows the testing program. The data is generated randomly within a certain range. Therefore, it does not look real, You can plugin your data. Check the code in the window class to see how to use those classes.

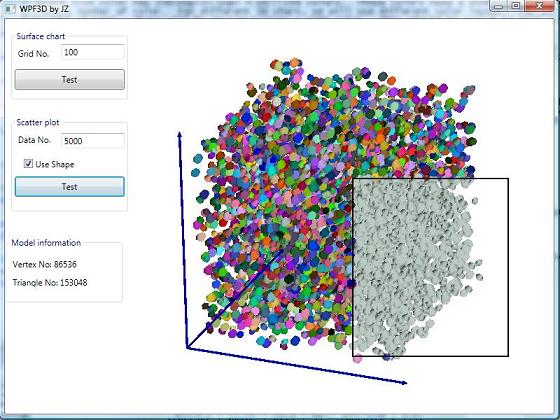
The project provides the following functions:

1. Generate a 3D model for display.

   Check the message handler for "Test" button to see how to generate the display model for 3D chart.

2. Rotate the 3D model.

   Hold the mouse left button to rotate the 3D model.

3. Drag the 3D model.

   Hold the mouse left button and shift key to drag the model.

4. Zoom

   Press "+" or "-" key to zoom

5. Select

   Use mouse right button to draw a rectangle and select data in the 3D chart.

x

WPF_3D_Chart_Source.zip

3 UCanCode Advance E-XD++ GIS SVG Drawing and Printing Solution Source Code Solution for C/C++, .NET V2023 is released!